深度解析!模拟与数字的桥梁——奈奎斯特采样定理
我的Bilibili频道:香芋派Taro
我的个人博客:taropie0224.github.io(阅读体验更佳)
我的公众号:香芋派的烘焙坊
我的音频技术交流群:1136403177
我的个人微信:JazzyTaroPie
Nyquist Shannon Sampling Theorem(奈奎斯特香农采样定理)
对于一个有限带宽且在时域上连续的信号,当采样频率大于信号中最高频率的2倍时,采样之后的数字信号完整地保留了原始信号中的信息。
假设我们有一个频率为1Hz的正弦波(sin(2pi*t)),根据采样定理我们能够得知我们必须要2个以上的采样点,这里我们就使用3个采样点,即采样率为3Hz。
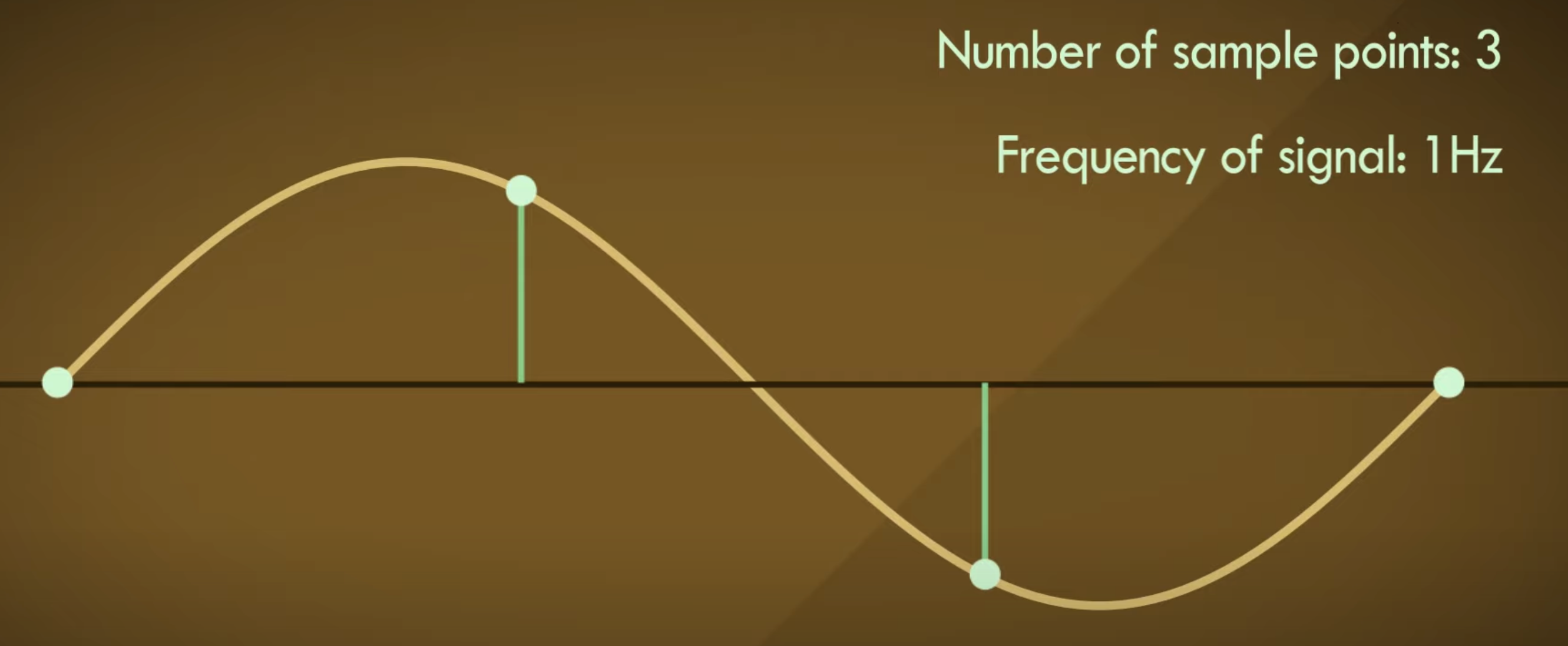
此时你肯定会想3个采样点显然不足以正确表示这个波,因为如果我们把它重新转换为模拟信号时,以下的几种情况似乎都是符合要求的:
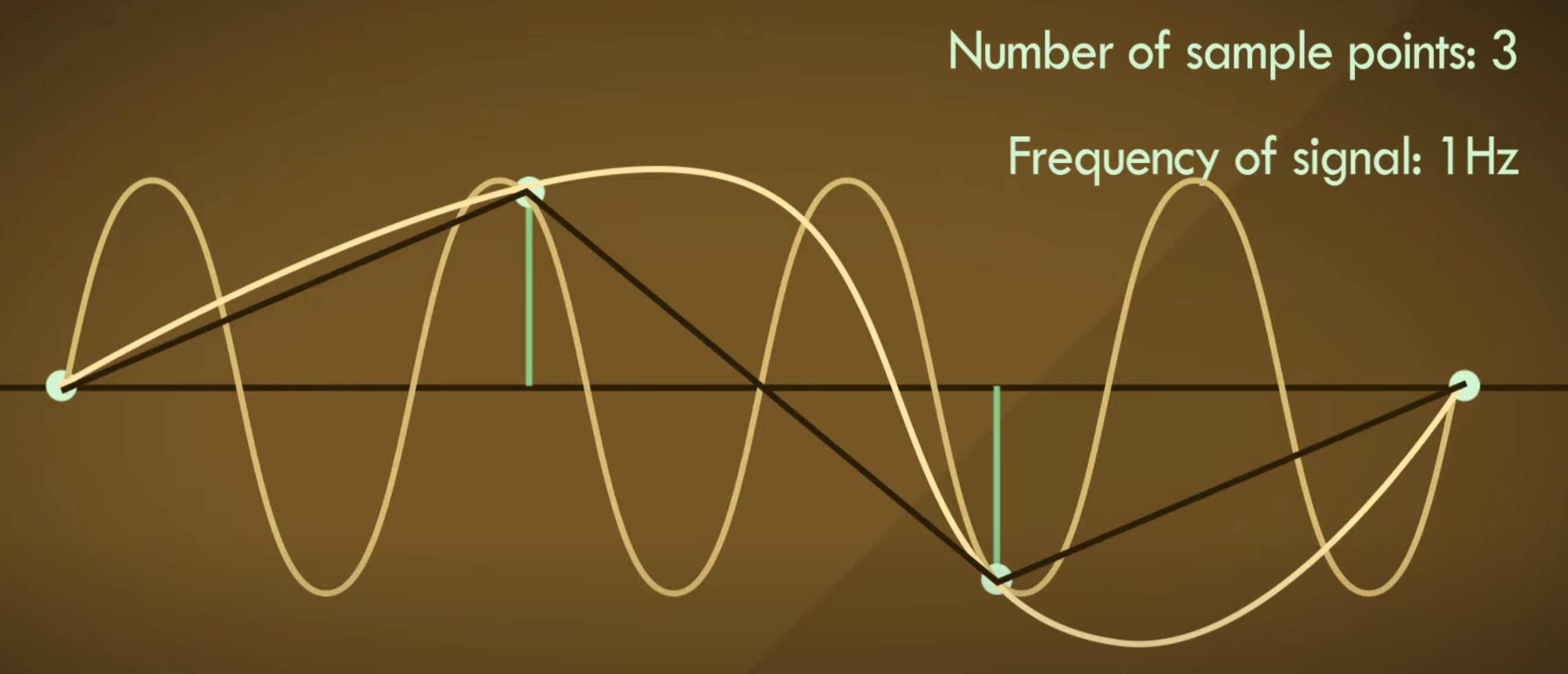
那要不再增加一些采样点,比如增加到40?情况似乎乐观了起来:

那么增加采样点真的能在重新转换为模拟信号时使信号更准确吗?答案是否定的。
很多人都有这样的误解:更高的音频采样率意味着更好的音质
采样定理证明了无论是3Hz还是40Hz的采样率,对于一个1Hz的正弦波来说,在把它重新转化为模拟信号时得到的结果是没有任何区别的。
是不是听着有些反直觉?
因为你在将数字信号转化为模拟信号时(采样时)其实是在做剥离信息并丢弃它的过程,但是当你重新将你采样得到的数字信号重新转换成模拟信号时,丢失的信息又是如何神奇地重新出现的?
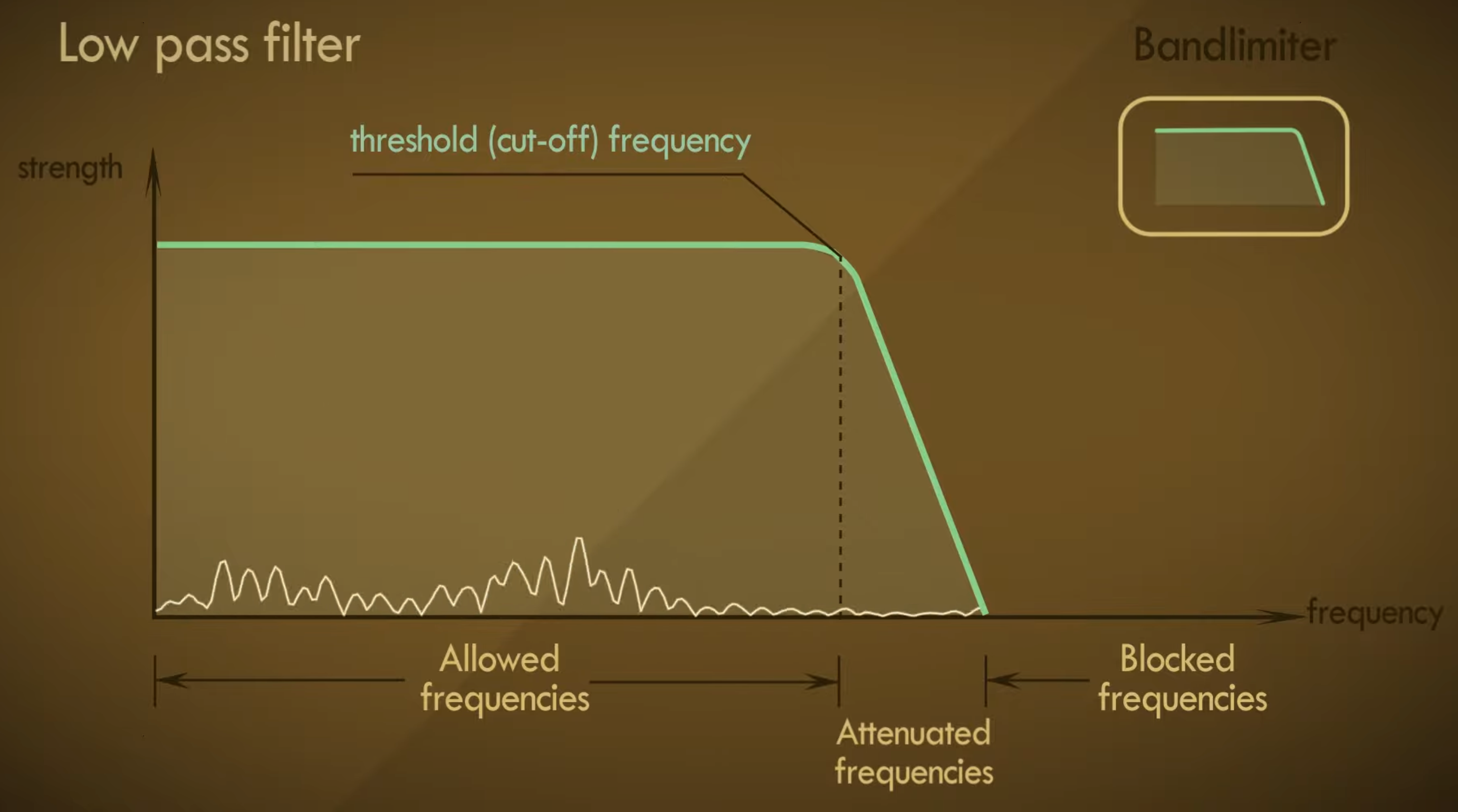
Bandlimiting(频带限制)
这意味着信号中所有大于1Hz的部分在ADC(模拟->数字)中被去除,而在DAC(数字->模拟)中再次被去除所有大于1Hz的频率分量,这可以用低通滤波器实现。

一个低通滤波器只允许信号中低于它截止频率的部分通过
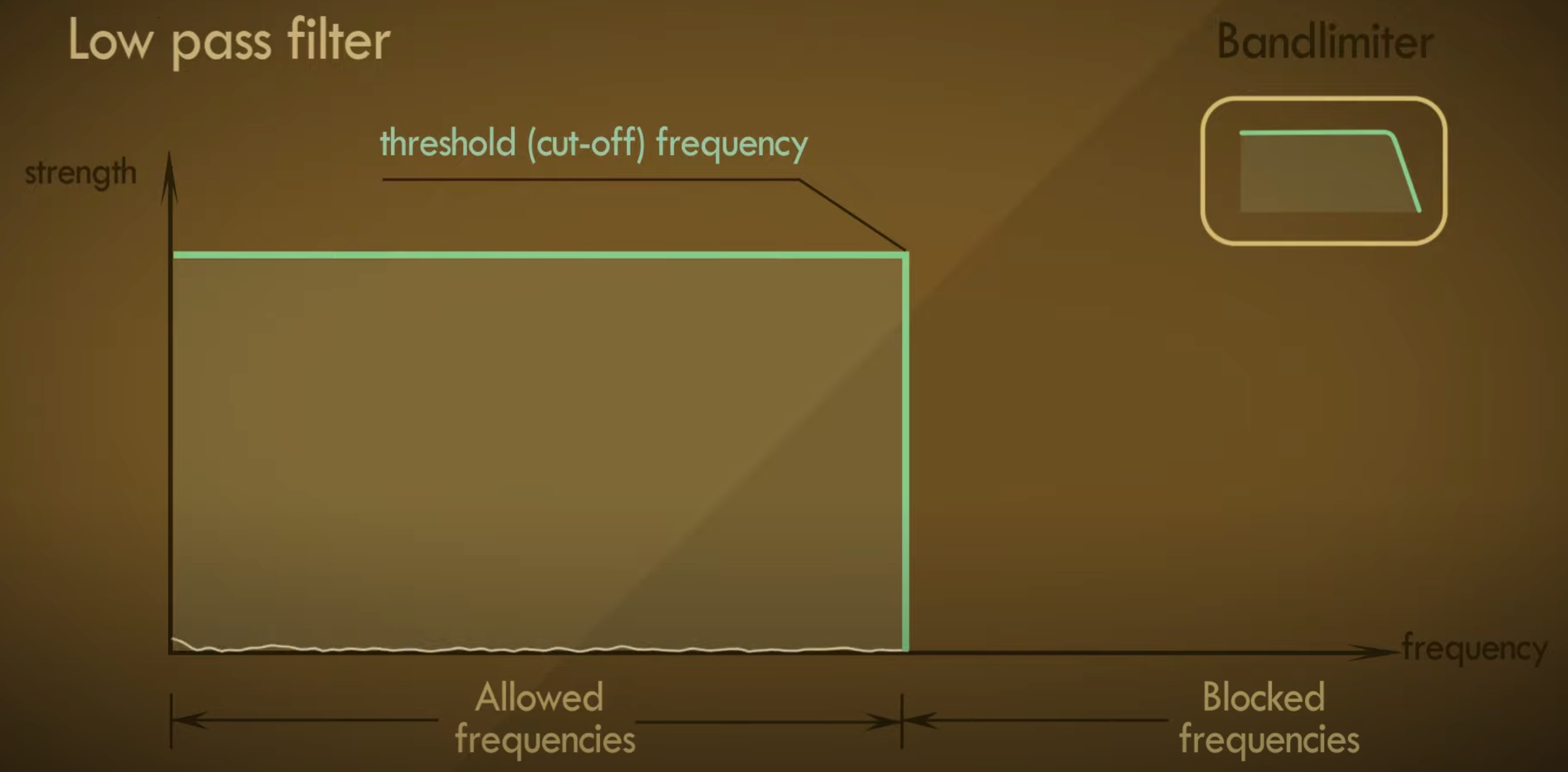
但是实际上低通滤波器是做不到这种类似一刀切的情况的,而是只能平稳地下降,这个问题在后文会有提到。
Sampling examples(举些采样的例子)
如果我们以正好最高频率2倍的采样频率采样时会发生如下状况:
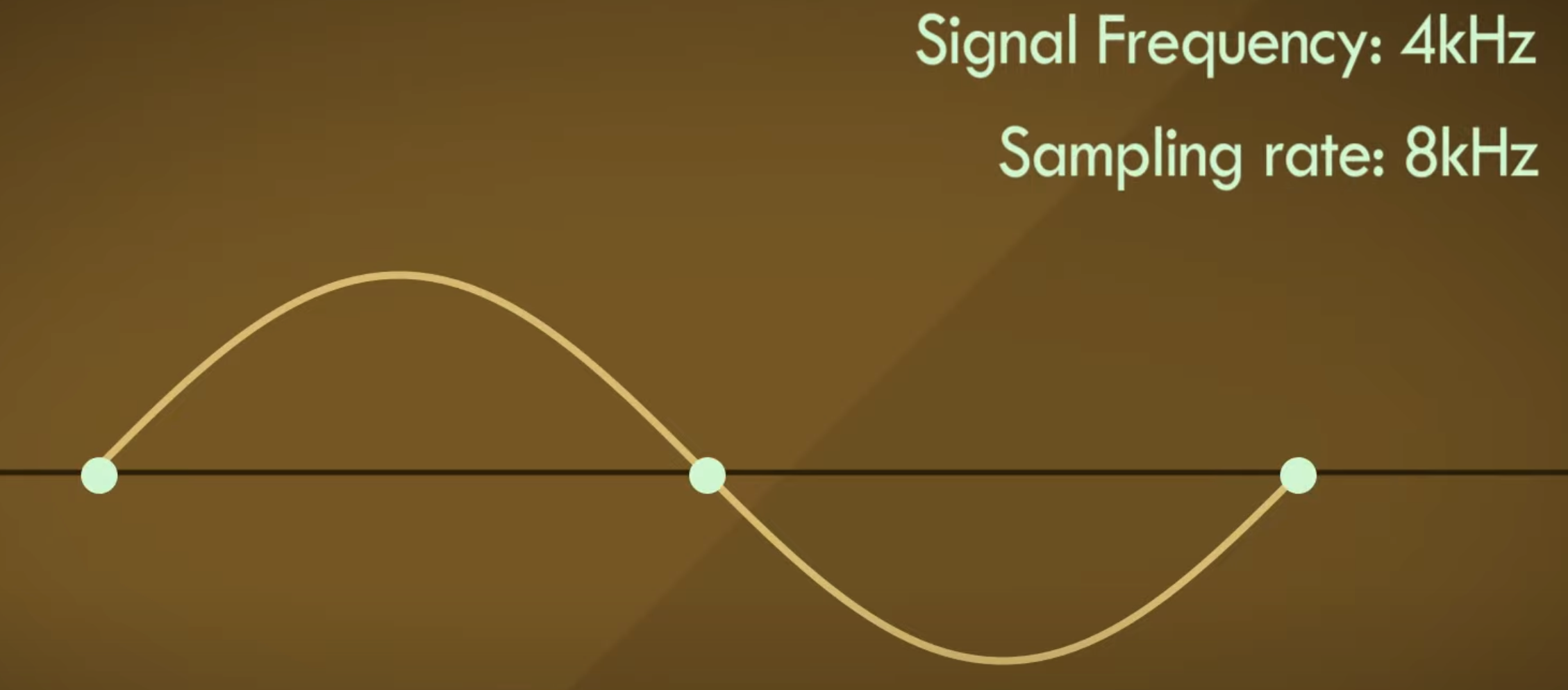
不幸的是,所有采样点都位于信号的零值点,这自然会被认为始终没有信号。
如果我们增加一些相位偏移呢?我们又得到了一个不一样的波形:
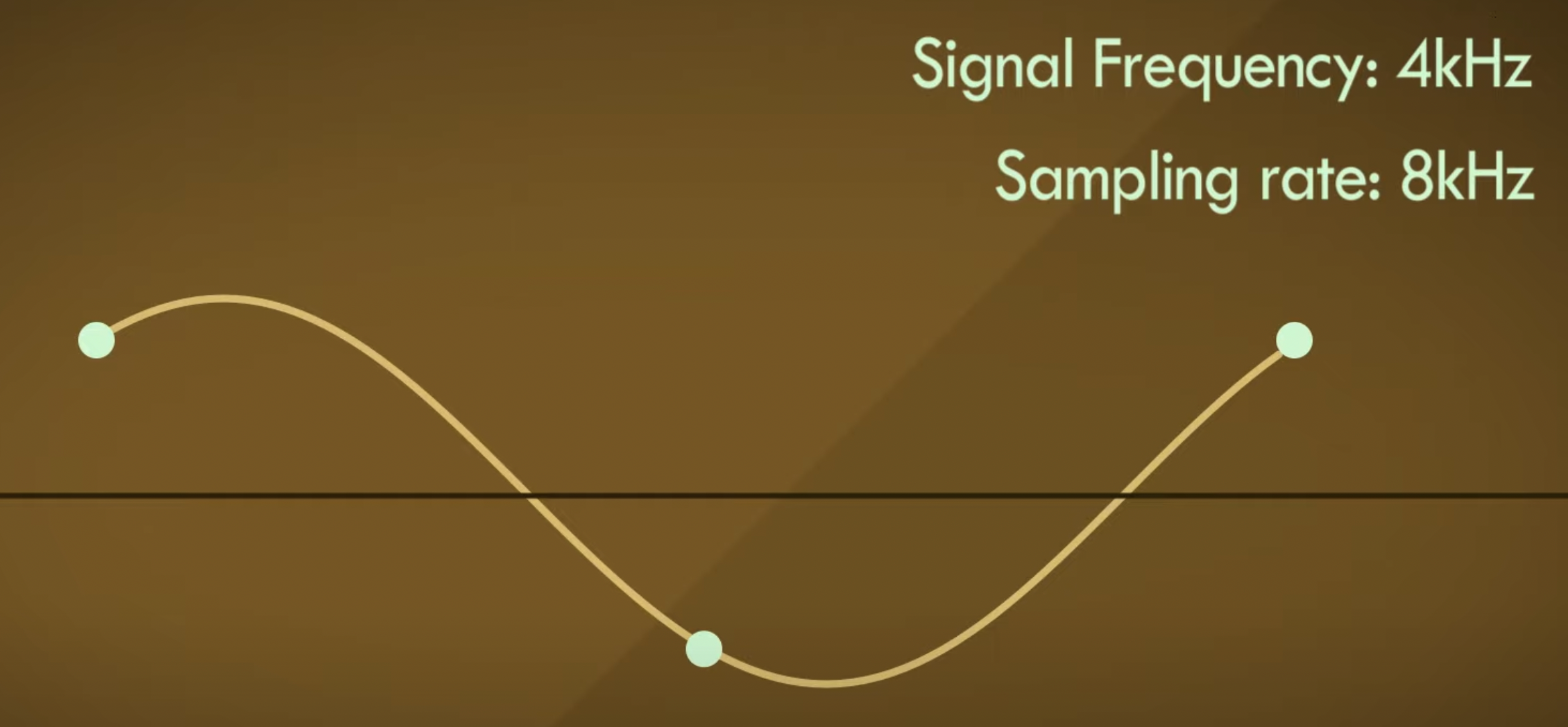
这就是为什么采样定理指出采样频率必须大于最高频率的2倍的原因,而不是大于等于
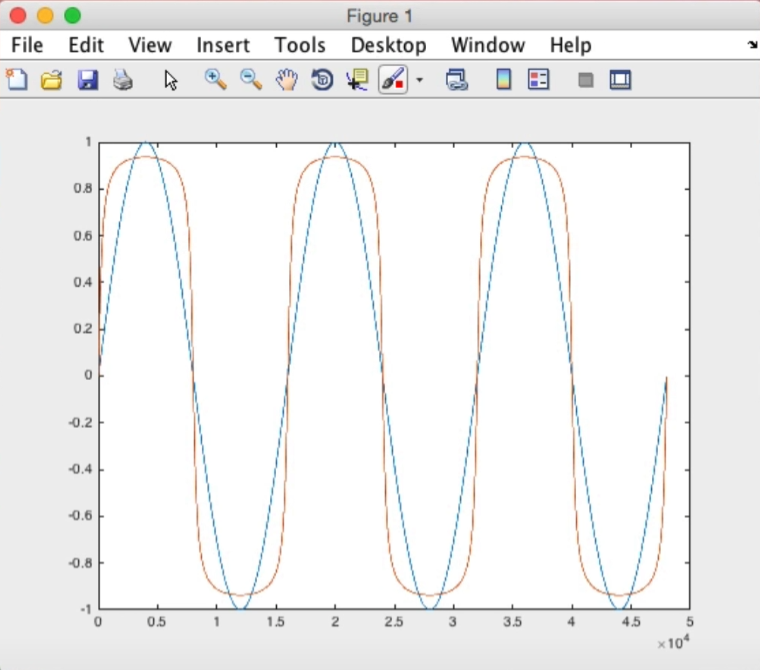
如果我们以不同的采样频率(均大于2倍最高频率)去采样一个3.999kHz的正弦波,软件会告诉我们如下结果:
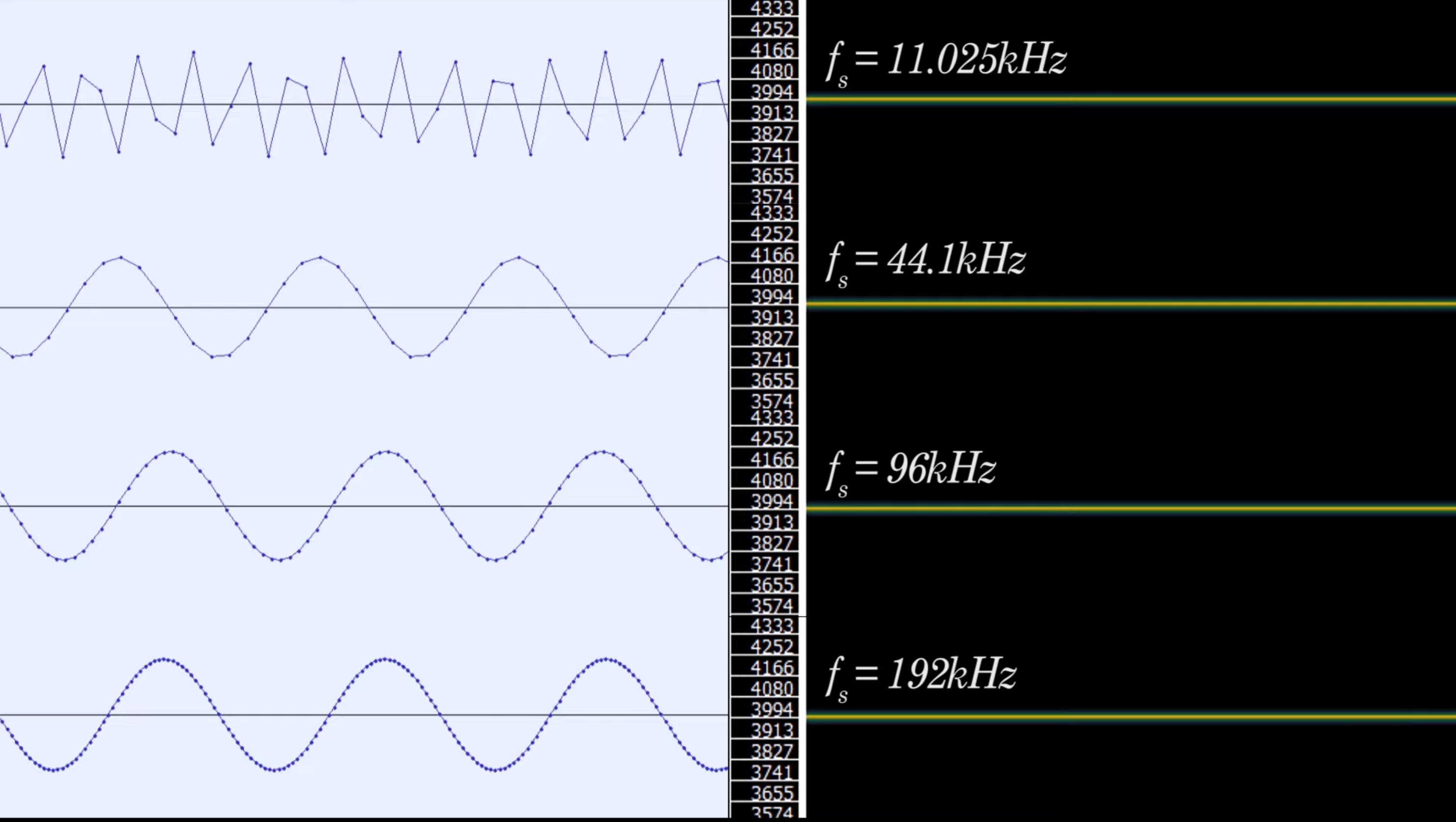
看上去采样出来的信号们长得还是不太一样,尤其是11.025kHz下这个信号好像有点抽象了,但是当我们播放试听时,似乎?没什么差别?
让我们来探讨一下为什么会这样
其实以上查看波形的方式是错误的,我们并不是在2个数据点间进行线性插值,即在两点间放置一条直线,这样的表示方式并不准确。
让我们将显示样本改为stem,这时我们才得到我们在数字领域所拥有的真正的离散数据:

现在当我们需要将此数字信号转换成模拟信号时供我们收听时,它会通过一系列电子电路。在最简单的情况下,它通过一个电阻梯形电路,产生中间模拟信号的阶梯模式:
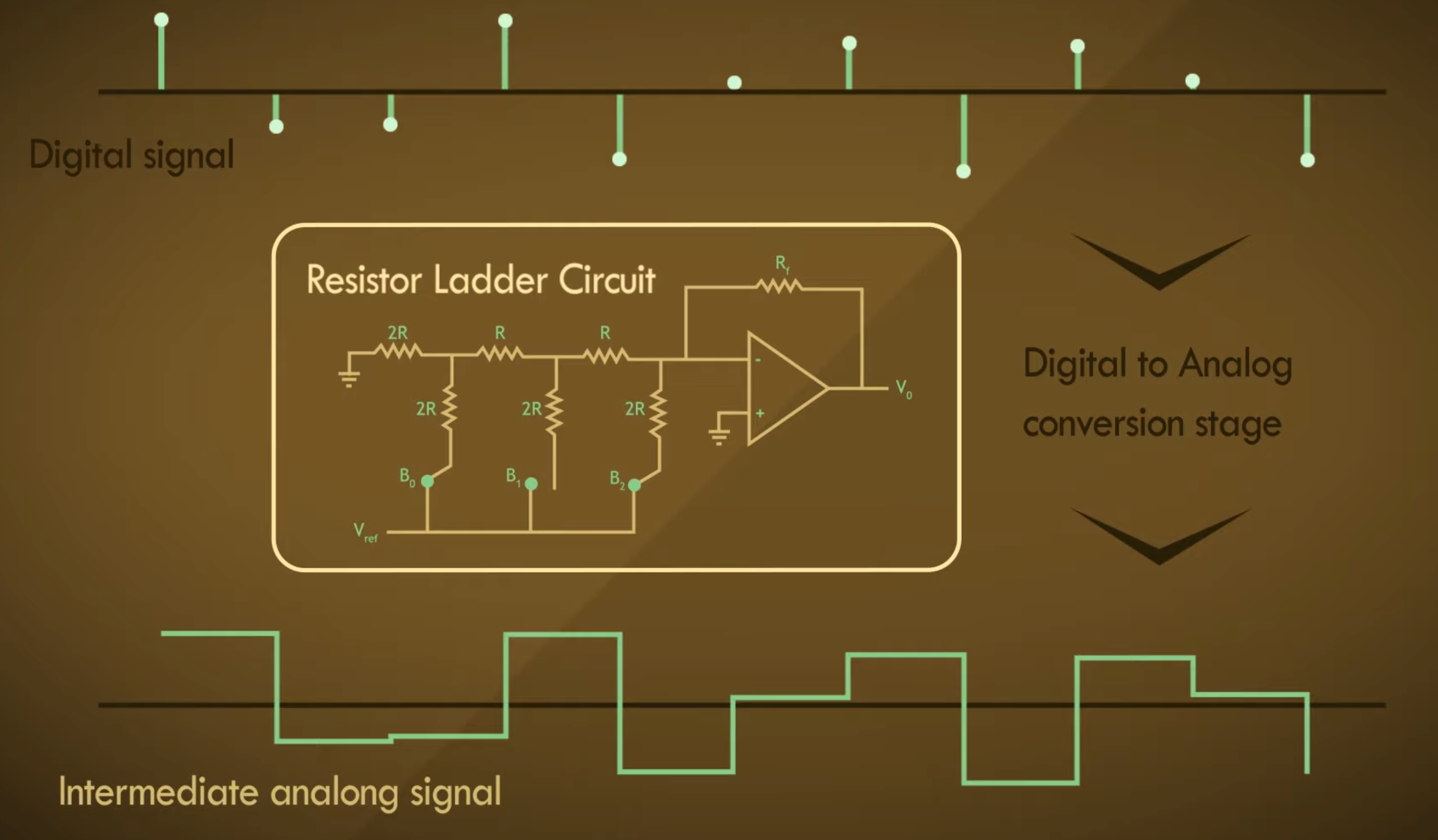
在这种形式下,模拟信号中有很多超高频成分,其中很多甚至是我们人耳听不到的。
但是对于这样瞬间变化的时域信号,扬声器的锥体必须根据信号快速移动。当此类事件偶尔发生时,通常会被视为咔哒声和噪声。但是如果它倾向于周期性的重复,你很可能会得到一个高频音调,而频率将取决于这种转变的斜率和高度差。
显而易见,现在我们必须切断这些多余的频率并丢弃它们,那么我们以什么依据来切断呢?
哦!我们又想起了之前我们采样时的过程,不如就以采样率的一半来作为切断的起点吧,这个点被称为奈奎斯特频率。
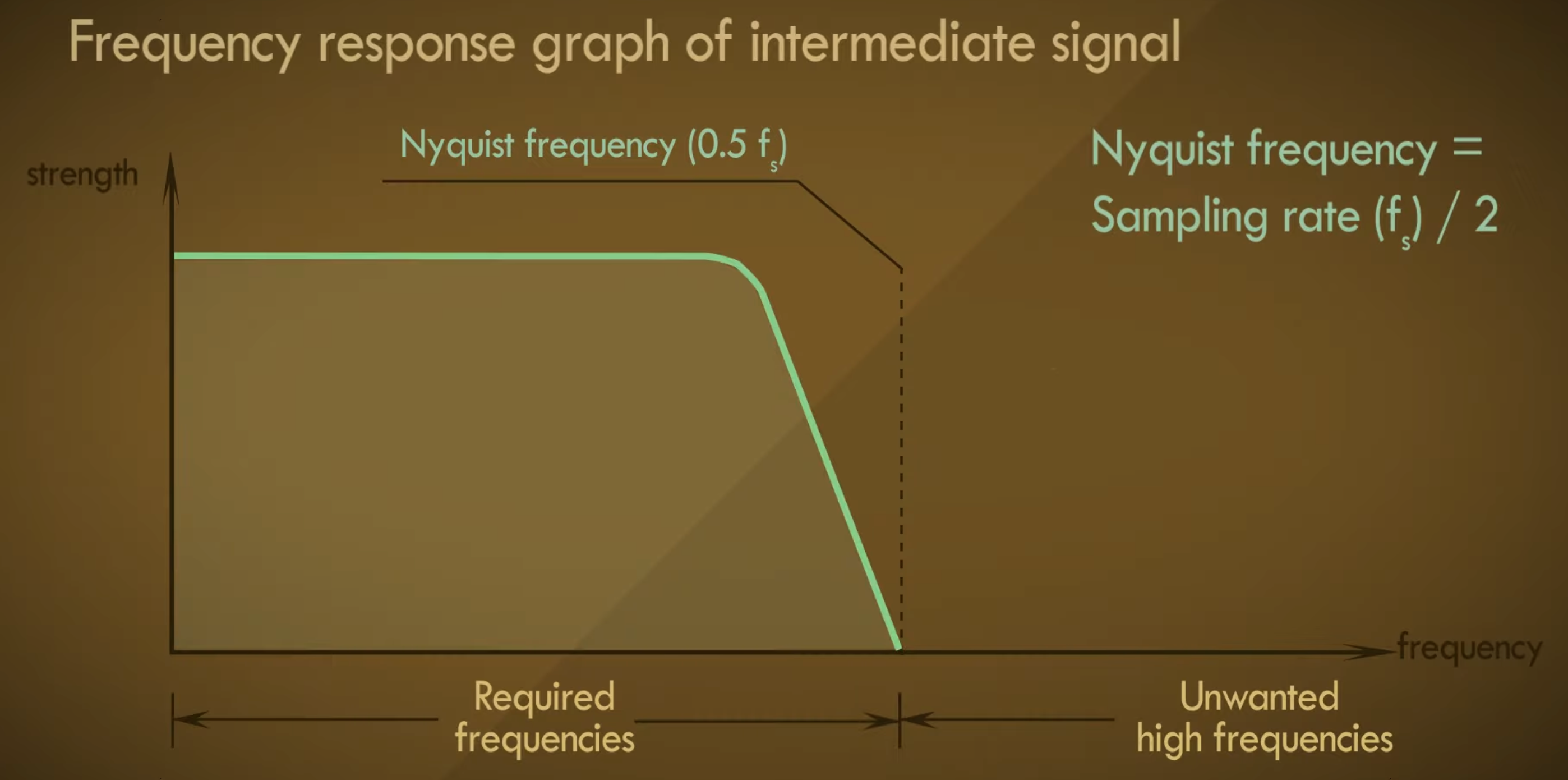
由于我们在对输入信号进行ADC的过程中“承诺”了放置一个低通滤波器,这个低通滤波器的截止频率就是奈奎斯特频率。自然在DAC的过程中也必须在奈奎斯特频率处有相同的低通截止。

当我们对之前的信号进行低通处理后,我们得到了最后的输出波形:
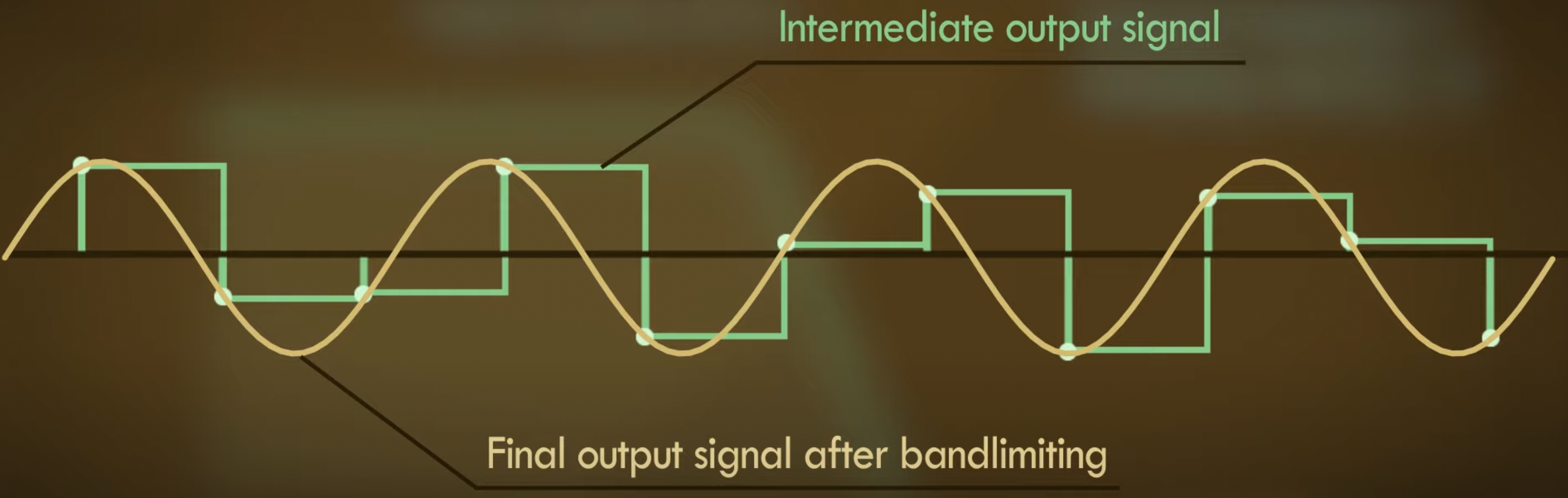
本质上它是一个平滑的版本,它与之前所有的采样点相交。
这就是事情变得有趣的地方,通过所有这些点产生的信号在数学上是唯一的解决方案,只有唯一一个有限带宽信号能通过所有采样点,它就是输入信号本身。因此,通过ADC的输入信号是唯一可能在DAC输出时产生的信号。
如果输出信号稍微偏离输入信号,这就意味着它一定包含高于奈奎斯特频率的频率,并且它不能满足采样定理中提出的关于频带限制的标准。
由此我们能够得到结论:转换在数学上是无损的
当然,模拟组件从来都不是无噪声的,但只要在转换次数保持在最低限度,这些噪声还是可以忽略不计的。
如果有机会的话,能够听到这个带有许多高频成分的Intermediate output signal一定很有意思,但很可惜的是,在电子电路中我们无法手动单独开关低通滤波器。
还没有结束
当我们在实验软件中以8kHz的采样率去采样一个3.999kHz的正弦波时,我们会得到这样的现象。
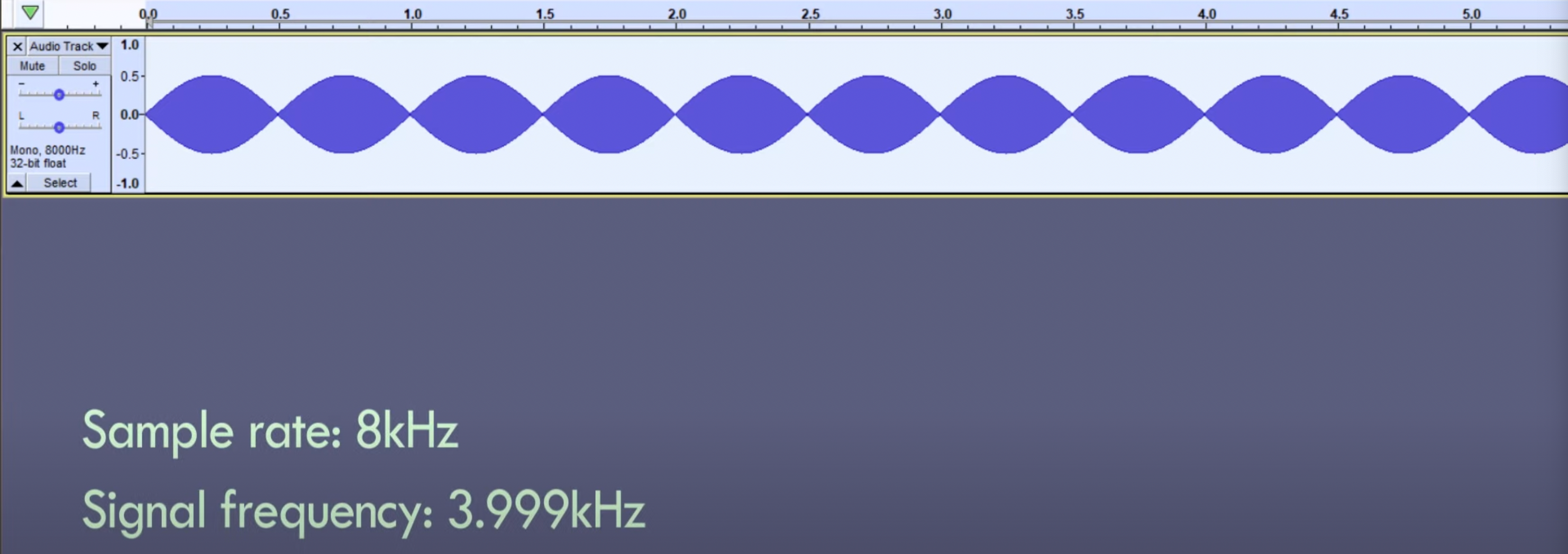
十分有意思的是,我们此时明明满足了采样定理,但好像并没有得到我们期望的采样后的信号,反而得到了一个在幅度上规律变化的信号,我们的采样似乎影响到了响度?
还记得我们之前在讲到低通滤波器时提到的不存在一刀切的低通滤波器的情况吗?问题就出现在这。

我们可以看到,由于在截止频率附近是一个平缓下降的过程,且我们的采样频率与奈奎斯特频率过于接近,导致了一部分我们在转换过程中需要被切除的高频部分没有被完全切除,而是变成了这个样子:
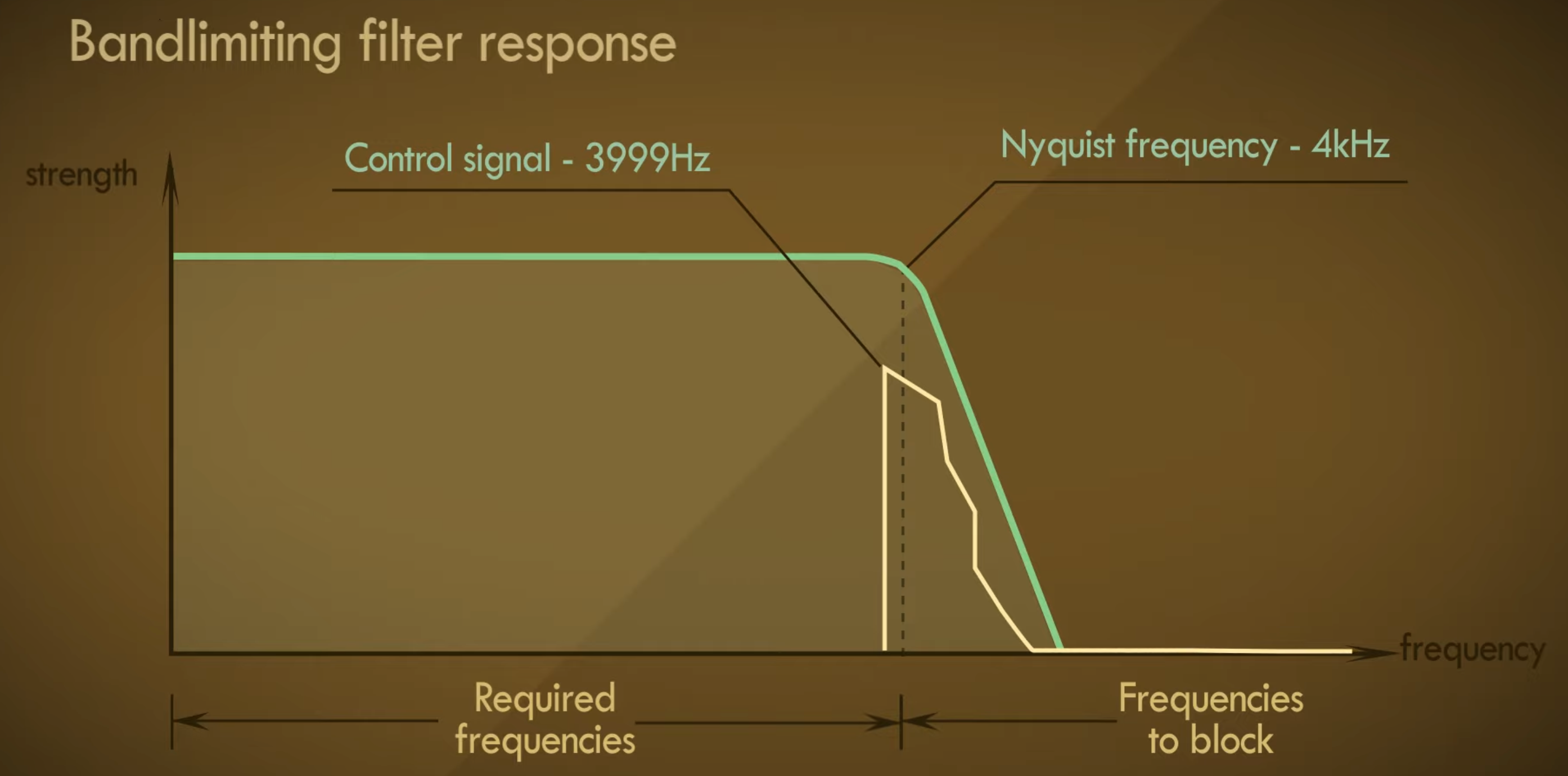
这已经违反了采样定理,因为采样定理要求没有高于奈奎斯特频率的部分。
这导致了一种混叠现象,我们将高于奈奎斯特频率的部分折叠回去
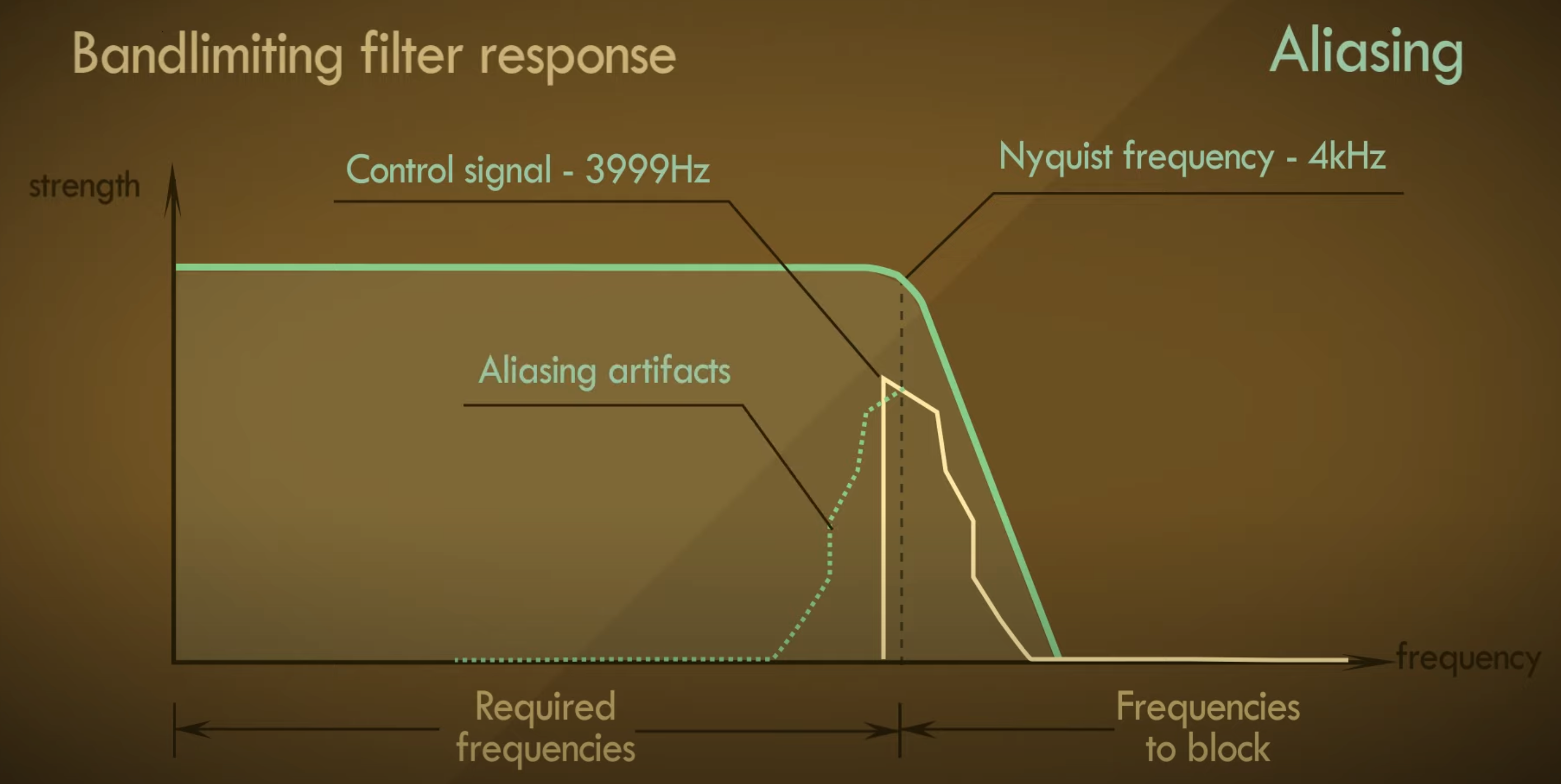
混叠将额外的频率添加到以前不存在的输出信号中,我们必须避免这种情况。
这种高于奈奎斯特频率的部分折叠回原始信号的情况导致了之前出现的幅度的变化
举一个很相似的例子,如果我们在一个较高的采样频率下(44100Hz)去采样得到一个400Hz和401Hz的正弦波,并把它们二者叠加,我们会听到一种称为Beating的声学现象:

它是由于两个频率略有不同的声音之间的干涉,导致的音量周期性变化的现象。
所以我们可以通过在信号最高频率和奈奎斯特频率之间预留一定的Buffer(缓冲)来避免这种混叠现象的产生:
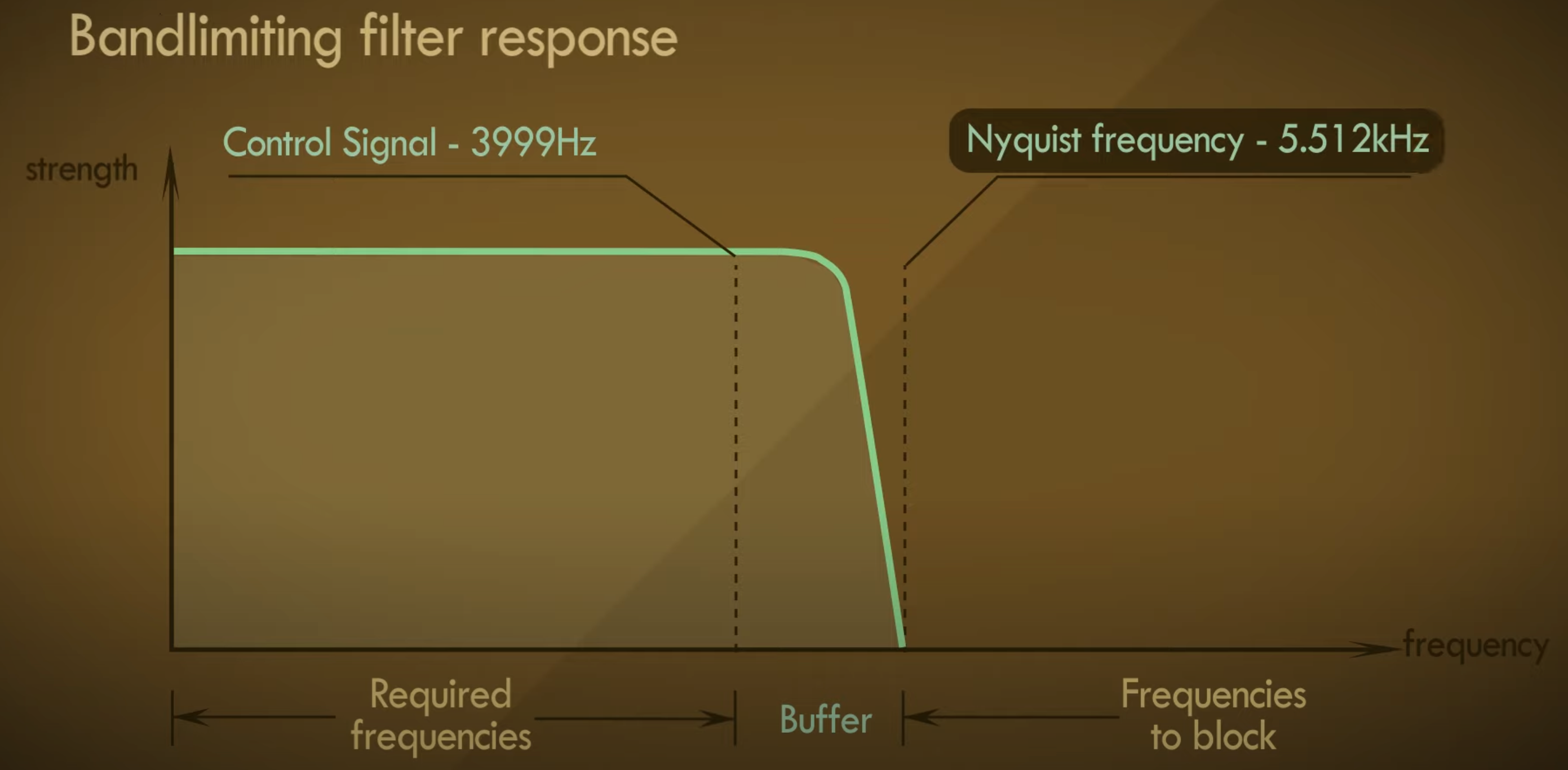
工程奈奎斯特定理由此产生,他将采样频率从最高频率的2倍提升到了2.5倍来换取一定的Buffer空间

感谢Akash Murthy提供的优质讲解和资料,欢迎关注他的Youtube channel: