前言

我的Bilibili频道：香芋派Taro
我的博客：taropie0224.github.io
我的公众号：香芋派的烘焙坊
我的音频技术交流群：1136403177
我的个人微信：JazzyTaroPie

（阅读此文章最好有一点点的DSP基础

你会算复利吗？

大家的初中数学老师应该都教过银行的复利怎么计算吧？

复利的一个特征呢就是当年的利息 = 上一年的本金 + 上一年的利息（图中的公式还计算了当年的新存款/取款，即**x[n]**），与单利最大的不同就是每年都会把上一年产生的利息重新加入总额再计算利息。

现在我们来换一种理财方式

假设小明觉得银行的活期利率太拉了，于是跟风在2006年1月1日购买了一款三年封闭管理的基金（自动续期），然后基金经理全仓梭哈了中石油，结果喜闻乐见地遇上了股灾，基金以每年-30%的情况在亏损。非常幸运的是，小明只买了1块钱，那么每年1月1日他账户里的钱就是这样的（账户存款为0即为钱都在基金里拿不出来）。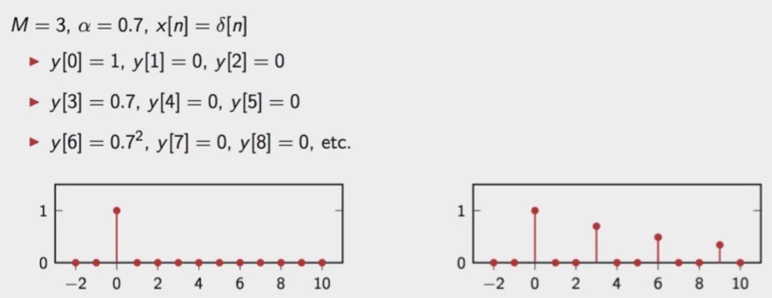

把他画成系统框图又是什么样子


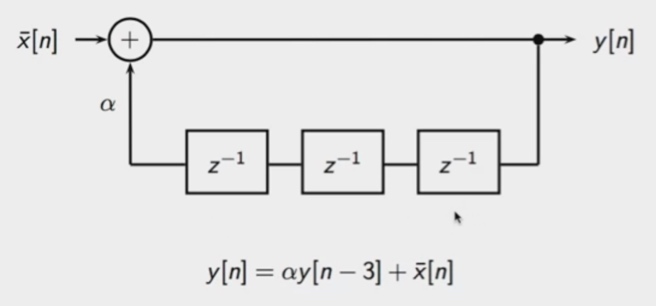
如果有一些DSP基础的同学应该很容易发现这其实就是一个循环，如果我们代入一下实际数值，得到的结果就是小明的账户发生的变化。
这里的x[n]是一个单位冲激响应，系统内有三个延迟器（M=3），α的值为0.7。显然，这是一个以3为周期无限循环无限长的序列。

同理，如果我们改变M或α或x[n]的值，也会有同样的规律。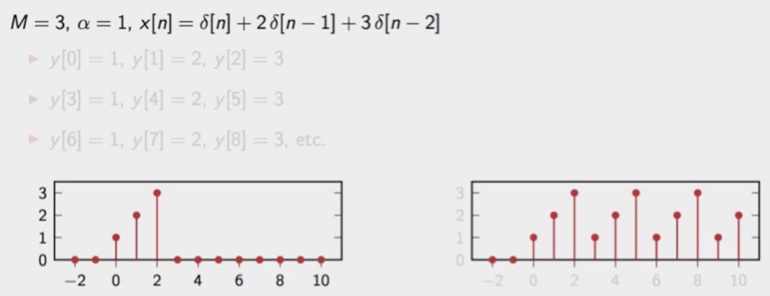

轮到我们的好朋友正弦波上场了

假设有这么一个sine wave被喂入到了类似的系统中：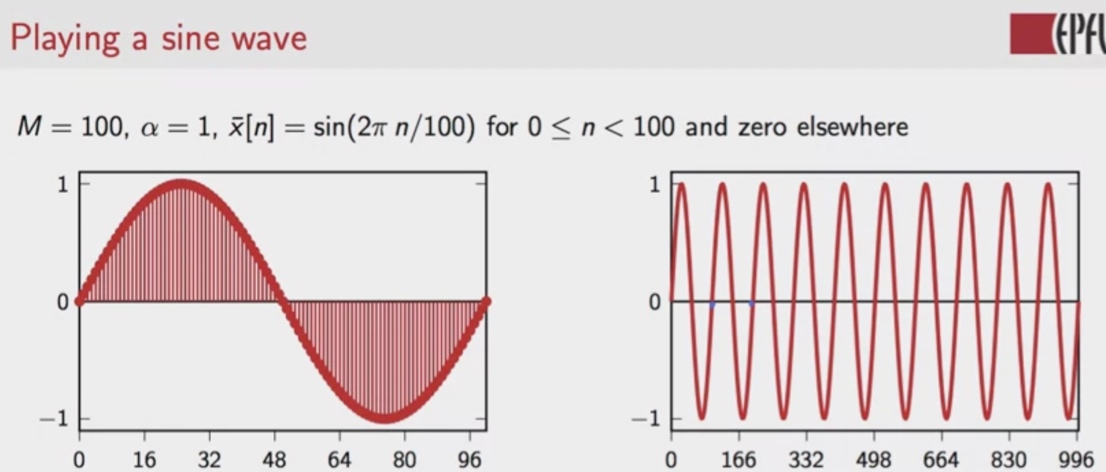

通过给出的数据我们能够知道，这个正弦波的周期为100，恰好与M相等，每次循环也没有任何的衰减（α=1）。如果当前的采样率是48kHz的话，我们也能由此推断出它的频率 = 采样率 / M = 480Hz。于是乎我们就得到了一个不断产生音高为480Hz的正弦波的振荡器。

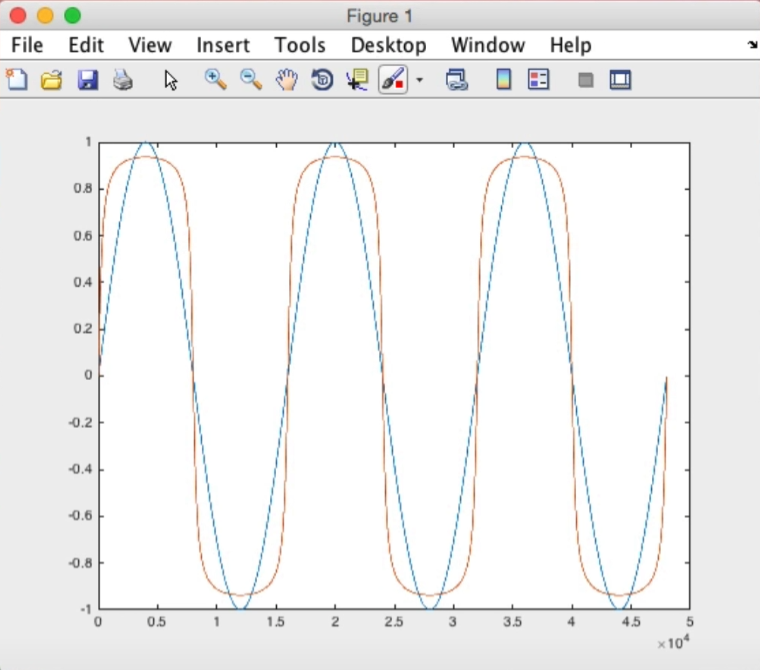
再来看一个它的好兄弟sawtooth wave（锯齿波）：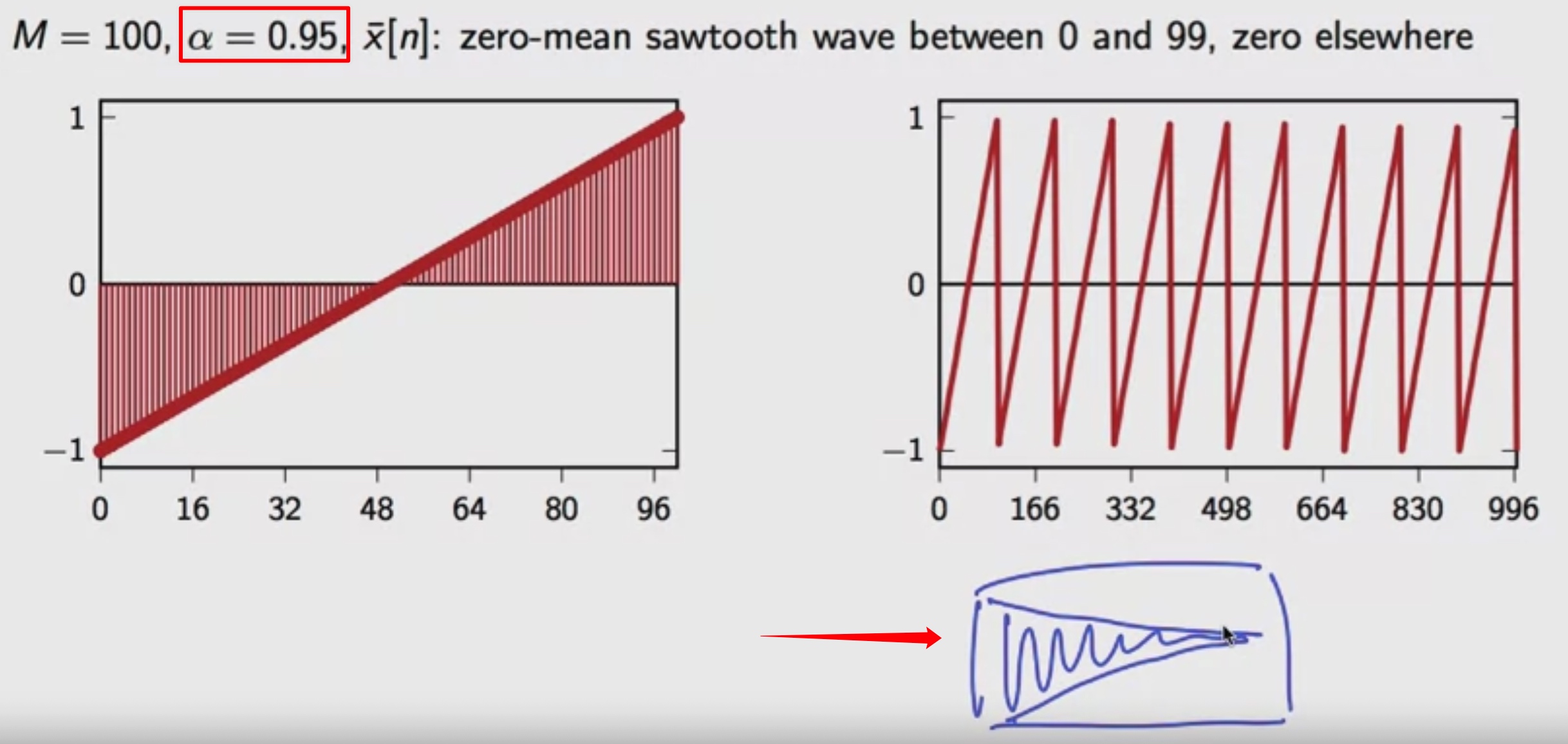

注意这里的α=0.95，表明它是会存在衰减的（每次循环衰减0.05），我们看到的波形就会像➡️指的那样。

我们似乎也明白了不同的参数分别控制着什么：


M对应pitch音高，α对应decay衰减，原序列对应timbre音色。

Karplus-Strong算法

是的主角要登场了！
我们的好哥哥Karplus认为使用白噪声在声音生成上会有更好的效果。你问为什么？
以下感谢知乎@DBinary的解答！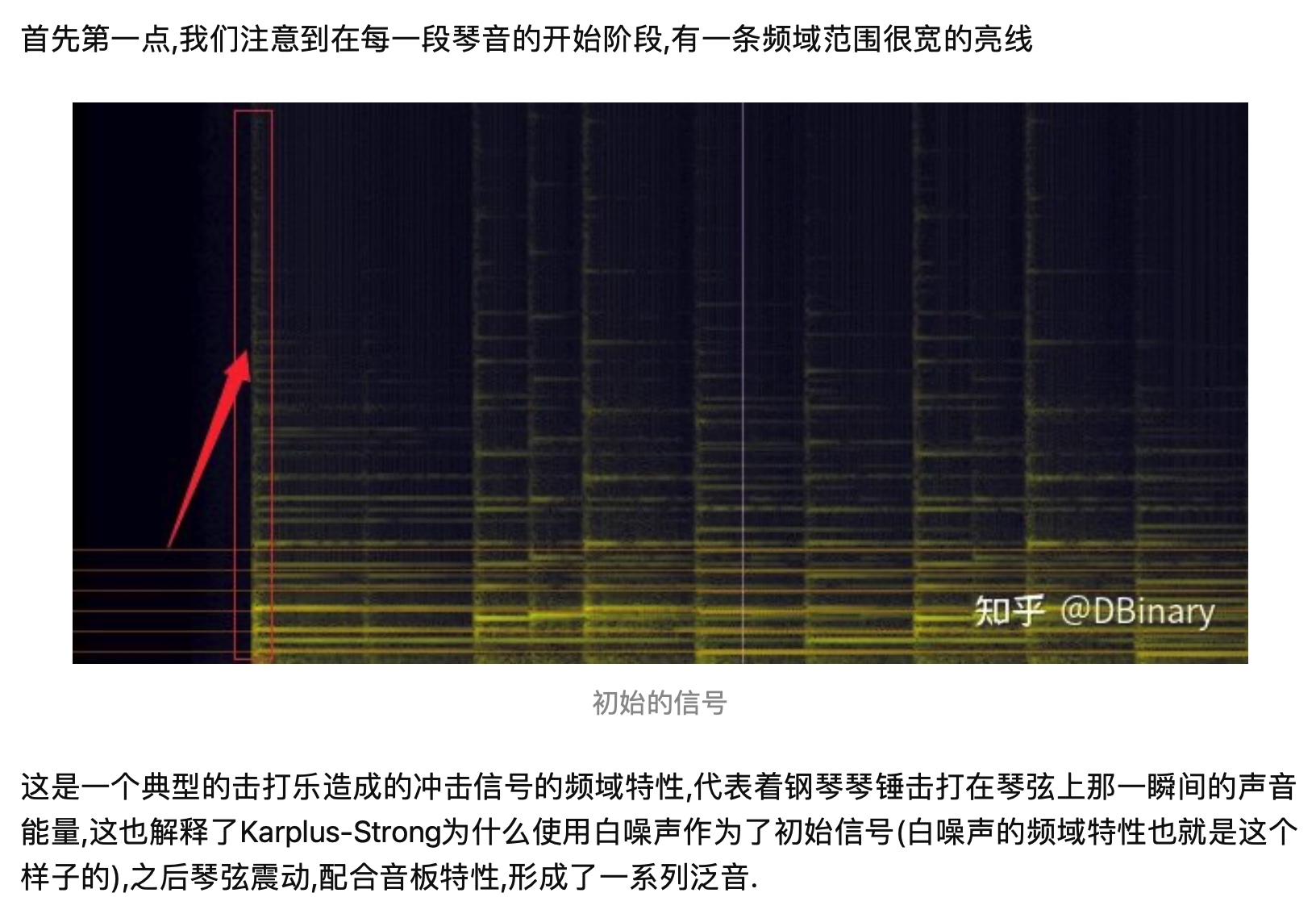

于是乎我们的波形变成了这个样子：

我们可以这样描述Karplus-Strong算法：

  1. 随机生成一段白噪声序列
  2. 按照x[i] = (x[i] + x[i-1]) * 0.5 * α的方式来处理整段白噪声，以此得到第一个基音周期的样本信号
  3. 重复该步骤直到需要的长度为止

我们可以发现在第二个步骤中出现了一个相加取平均的过程，这是由于对于离散信号取平均相当于加了一个低通滤波器，我们在上面的频谱图也可以看到，乐器高频信号的能量衰减要比低频信号的能量衰减快许多。

我们还知道泛音对于音色的影响是极为关键的，Karplus-Strong通过不断构造基音信号（有衰减）形成一个以基因周期为基准的泛音信号。

嗯，大概原理就是这么一些。

一种优化思路

原来呢是这个样子的：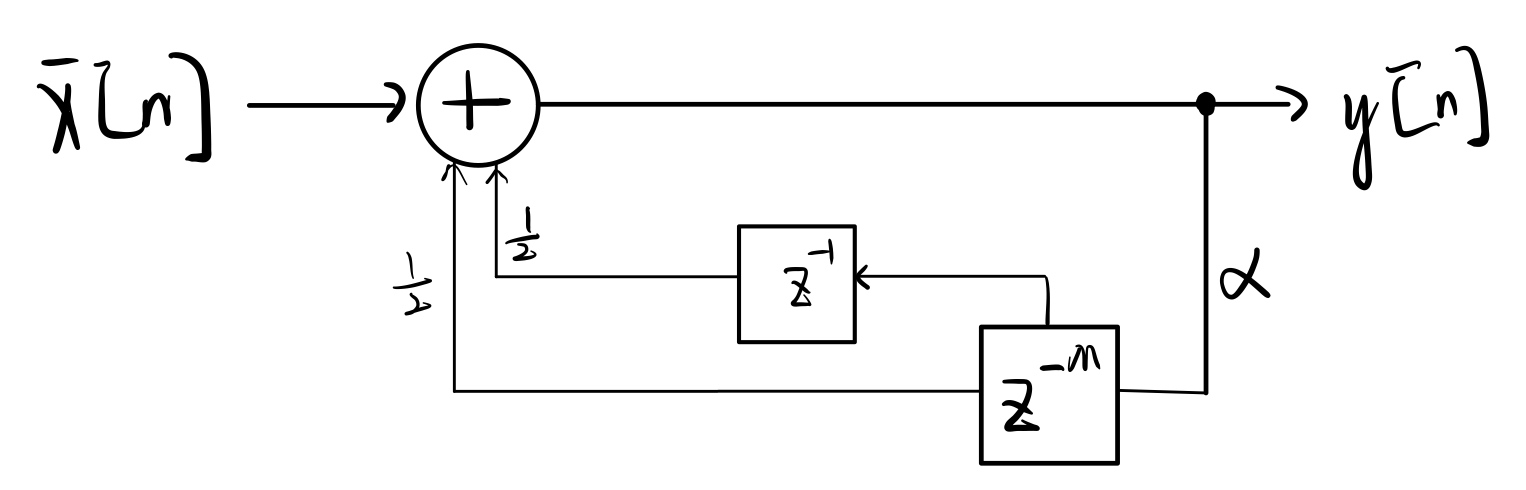

但是我们可以在这个相加平均的地方动一些手脚，把它改成这个样子：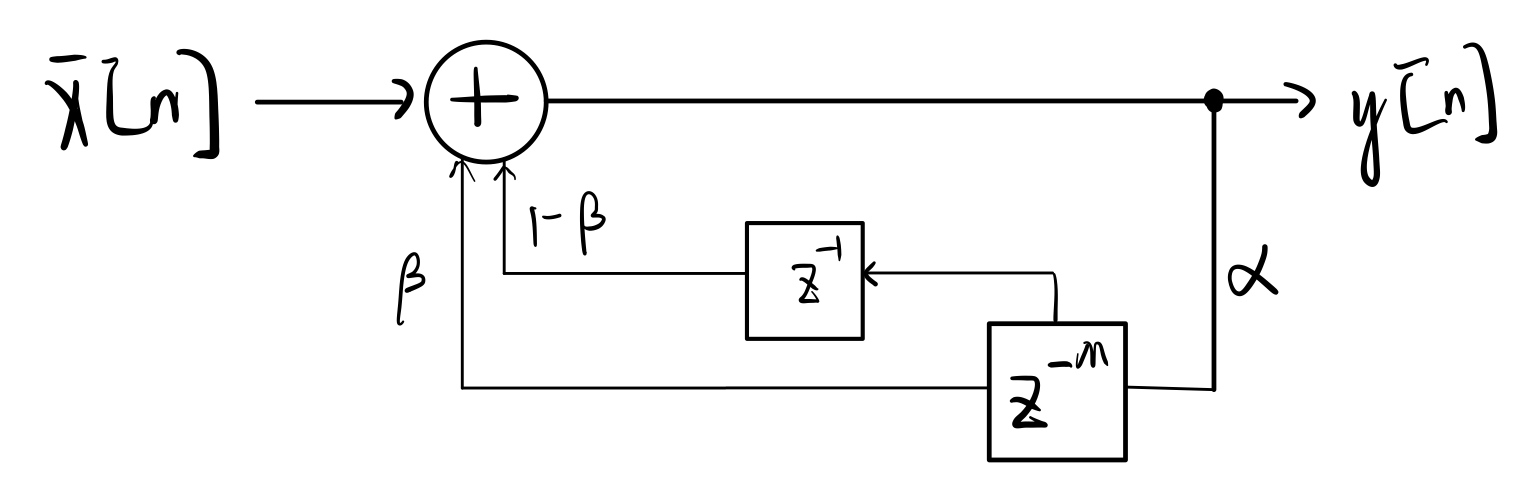

图中β的取值为(0,1)，β的取值越小，合成音色听起来越像吉他；β的取值越大，听起来越像扬琴，其本质是改变高频与能量的衰减速率。

总结

在Coursera重学DSP的时候看到了这个算法，就稍微深入地研究了一下，每次我看到这种算法的时候都会感叹发明的人真是天才，完美地实现了模仿一个音色几乎所有的调参，重要的是公式十分简单！当然，他还是有弊端的，比如有些乐器的高频衰减不同，时域能量的衰减方式也不是线性的，所以还是需要优化滴。